对它的追求一直没有停止

是的，自从圆这个美妙的图形被发现后，人们对的追求就一直没有停止过。

先带大家回顾一下小学的知识：圆的周长与直径的比是一个定值，就是（圆周率），用公式表示就是：。

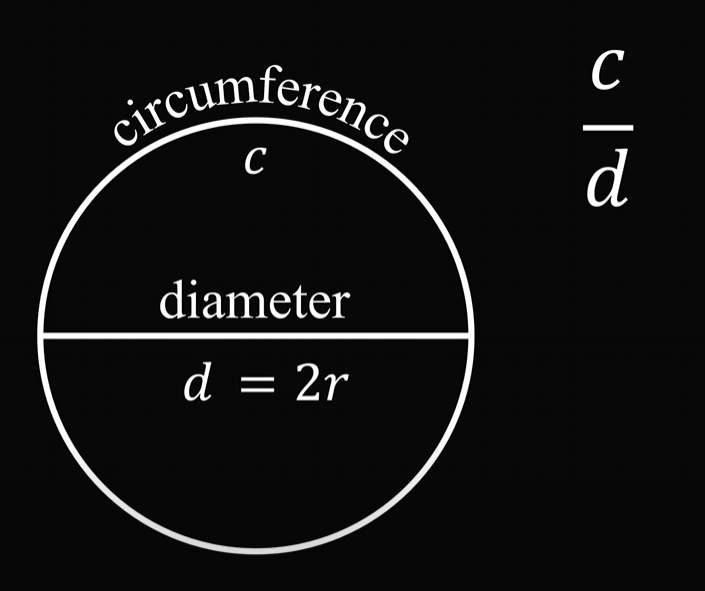
公元前250年左右，阿基米德通过对圆做一个内接六边形和一个外切六边形，并计算两个六边形的周长，框出了的大概范围：，然后通过不断内接和外切更多边的正多边形，将的值第一次精确到。

中国古代的数学家刘辉在约263年、祖冲之大约在450年的时候，第一次将圆周率精确到小数点后六位（3.1415926和3.1415927之间）。两人使用方法的原理和阿基米德类似，但他们不是用周长近似而是用面积近似，因此才能得到更高的精度。祖冲之还给出了一个容易记忆的近似值：355/113（113355中间断开，一个当分子，一个当分母）。

这个记录保持了1000年左右到了15世纪，此时一位阿拉伯数学家卡西将圆周率算到了小数点后17位。

不过，用这种几何方式来求圆周率到了极限。数学家们要找到更有效的方式去求圆周率。¹

差不多到了14世纪中的时候， 印度数学家Madhava第一次用无穷级数来表示了圆周率，这个公式值得写出来，因为它很简单：

这位老兄将圆周率一直算到了3.14159265359……及更多。

这个公式有一个很大的问题，就是它收敛起来太慢了。收敛的意思是，要得到某一位精确的圆周率数值，你可能要算几亿次！效率太低：要精确到小数点后10位，需要计算50亿次！

所以，现在数学家们都用更有效率的算法，来计算圆周率。这个算法来自1887年出生的印度数学顶级天才拉马努金（Ramanujan），并由乌克兰裔美国数学家楚德诺夫斯基改进。这个公式也非常值得写出来：

数学家们用这个公式，借助大型计算机，将圆周率算到了小数点后100 trillion（100万亿）位！

说实话，这么精确的圆周率没有啥实际用途，一般只是用来“炫耀”计算能力而已。

一直以来，数学家们还在寻找更多能表示圆周率的公式。

差不多在10天前，两位印度物理学家（是的，两位物理学家！）在研究弦理论在场论中的拓展时，“意外”发现了一个求解圆周率的新公式，而且速度更快——只要计算30次，就能将圆周率精确到小数点后10位！大家对此都表示欢迎和期盼。

我们先来认识一下这两位老兄，左边是Aninda Sinha，右边是Arnab Saha。

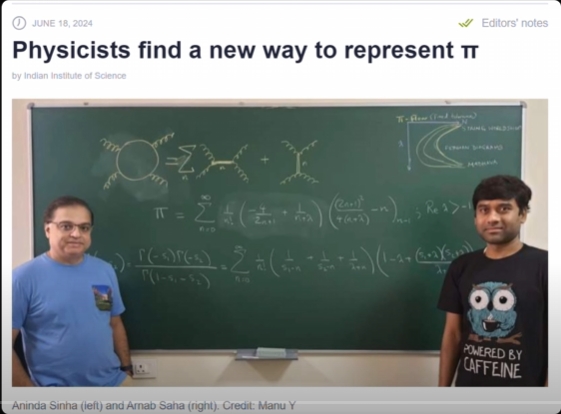
我们来欣赏一下这个公式：

对这个公式的详细解释已经超出了我的数学范围……有兴趣的同学可以参考两人的这篇论文。

今天的数学知识普及就到这里！